수학 가형 190619

주의. 이 게임은 요령 없이 하다간 저절로 똥손, 똥발이 되어버리는 존나 어려운 게임입니다. 이 게임은 존나게 어려워서 몇 번이고 유다희 누님을 영접할 위험이 있습니다. 계속하면 정신이 나가 샷건을 칠 수 있으니 하기 전에 다량의 항암제를 준비하거나 전문가와 상의를 권고합니다. 하지만 이미 늦었군요, YOU DIED

개요

2019학년도 6월 평가원 모의고사 수학 가형 19번 문항이다.

전통적인 킬러배치 번호인 21, 29, 30번대 문제가 아님에도 불구하고 난이도가 높게 나온 문제이다. 때문에 정답률이 매우 낮다.

29번 30번은 또 쉽게 나왔던 시험이라, 사실상 이 문제가 眞킬러 아니냐는 소리가 많았다.

문제 분석

0이 아닌 실수 p에 대하여...

일단 실수 p는 0이 아니라고 한다. ㅇㅇ 그래 시발

두 포물선 x2 = 2y와  (y + 1/2)2 = 4px에 동시에 접하는 직선의 개수를 f(p)라 하자.

f(p) 어쩌고 하니까, p값에 따라서 동시에 접하는 직선의 개수가 달라지는 것 같다. 그리고 우리는 그걸 관찰 해야하고

마지막에 구하라는건 f(p)의 우극한 값을 f(k)보다 크도록 하라는 건데, p값에 따라 동시에 접하는 직선의 개수를 관찰하면서 f(p)의 개형을 알아내는 것이 우리의 과제가 될 것같다.

풀이

Phase 1

뭐 이 문제를 그림을 일단 그려서 푸는 사람도 있겠지만, 기하적으로 고정적이고 이차곡선의 정의를 활용하기 유리한 문제가 아니고서야 그냥 수식으로 푸는게 정신건강에도 덜 해롭다. 그리고 이거 생각보다 시험장에서 중요한 마인드다.

동시에 접하는 직선의 개수라니까 헷갈릴지 모르겠는데 어찌되었건 뭔가의 접선이라는거다. 즉 한 곡선을 정하고 접선의 방정식을 일단 세우는게 첫번째 과제이다.

x² = 2y

(y + 1/2)² = 4px

둘 중에 뭐로 접선의 방정식 세우고 싶냐? 이런 문젠데

변태가 아니고서야 위에꺼 하겠지? 위에껄로 세우자.

위의 식을 미분하면

dy/dx = x

접점의 x좌표를 t라고하면, 접선의 방정식은

y = t(x - t) + 1/2t²

y = tx - 1/2t²가 된다.

이제 저 식을 또다른 곡선 (y + 1/2)² = 4px과 연립해서 나온 2차식의 판별식이 0이면

두 곡선에 동시에 접하는 접선의 조건이 된다.

이제

y = tx - 1/2t² ...(1)

(y + 1/2)² = 4px ...(2)

이 새끼들을 연립해서 섹스해야하는데

y를 소거해도 되긴 하지만, 뭔가 (y + 1/2)²의 안에 항이 세개가 들어가서 그걸 또 전개하는 불상사보다는 그냥 x를 소거하는게 나아보인다.

변태라면 y를 소거하셔도 좋다.

x를 소거하기 위해서 (1)식을 x에 대한 식으로 정리하면

x = y/t + 1/2t 이다.

냅다 (2)식에 대입하면

y² + (1 - 4p/t)y + 1/4 - 2pt = 0 (단, t≠0)

판별식D = 0을 세우면

D : (1 - 4p/t)² - 4(1/4 - 2pt) = 0

8pt - 8p/t + 16p²/t² = 0

p ≠ 0이므로, 양변에 t²을 곱하고 p²을 나누면,

p = - 1/2t³ + 1/2t

Phase 2

y = p ...(1)

y = - 1/2t³ + 1/2t ...(2)

에서 p값을 움직여가면서 t의 교점개수가 몇개냐를 관찰하는 것이다.

여기서 t의 교점 개수가 p값에 따른 접선의 개수가 된다.

(2) = g(t)라고 하고, g(t)를 t에 대해서 미분하면

g'(t) = - 1/2(√3t + 1)(√3t - 1)

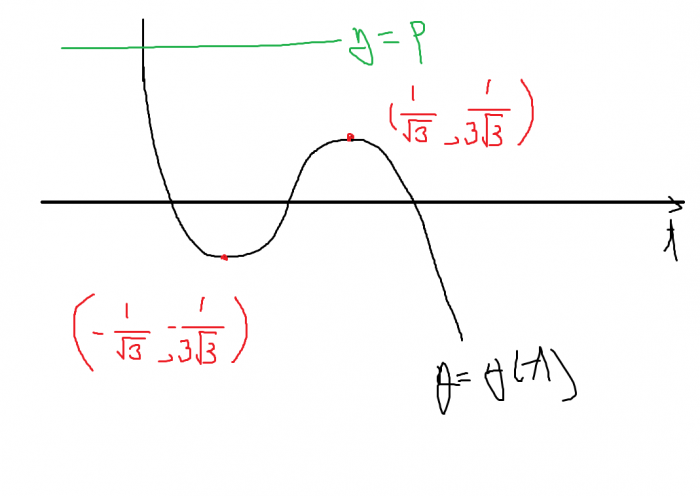
이대로 그래프를 그려보면 상황은 다음과 같이 된다.

그래프를 관찰하면 다음과 같은 결론을 얻는다.

(p > 1/3√3) ... f(p) = 1
(p = 1/3√3) ... f(p) = 2
(-1/3√3 < p < 1/3√3) ... f(p) = 3
(p = - 1/3√3) ... f(p) = 2
(p < - 1/3√3) ... f(p) = 1

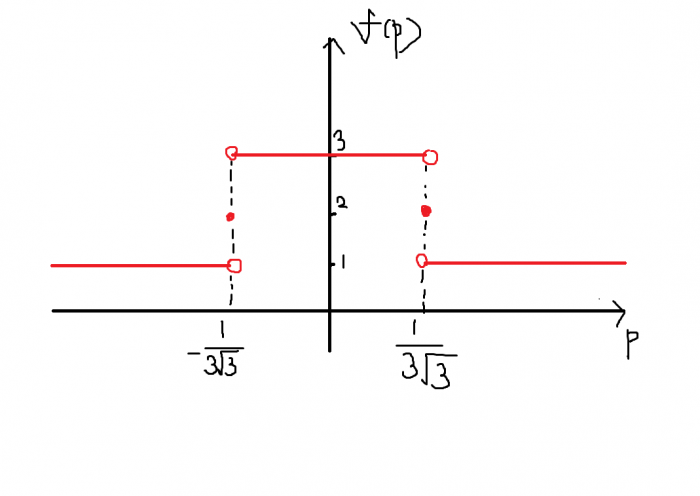
따라서 f(p)의 그래프는 다음과 같다.

우극한이 함수값보다 클 수 있는 경우는 - 1/3√3 뿐이다. 따라서 k = - 1/3√3이고,

- 1/3√3 = - √3/9 이므로

답은 3번이 된다.

평가

계산량이 극혐이라 시험장에서 AFK를 많이들 쳤던 문제이다.

근데 어쩔 수 없다. 정면으로 부딪쳐라.

이차곡선의 접선이 교육과정에서 분명히 빠졌을텐데도 표정 하나 안바꾸고 그냥 출제를 해버렸다. 걍 공부할 수 있는건 다해라.