|
이 적절한 문서는 적절합니다. 이 적절한 문서의 적절한 내용은 적절히 적절하기 때문에 적절하지 않은 당신도 적절히 적절하게 됩니다. |
개요
2014학년도 6월 평가원 모의고사 수학 B형 21번 문항이다. 2009 개정 수학 삼각함수 극한 문제 중에서는 어려운 편으로 평가받는다.
문제 분석
2차 평면 상의 도형 문제는 점이 태어나는 과정을 살펴봐서 최대한 점과 점사이의 거리나 각조건을 뽑고, 세 점씩 위치관계를 파악하여 삼각형의 형성을 꾀하는 것이 기본이다. [1]
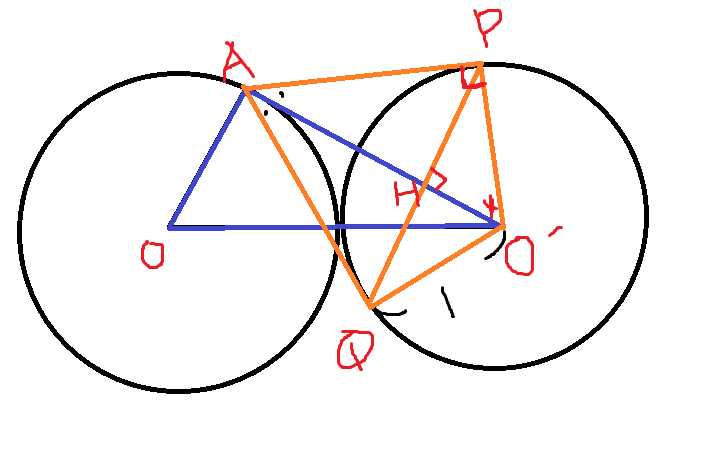
O, O' 이 먼저 형성되었고, 각 점을 중심으로 똑같은 반지름 1의 두원을 접하게끔 형성하였다. 선분 OO'의 길이는 2이다.
선분 O'P = 1, 선분 O'Q = 1, 선분 OA = 1 이다.
각이 세타로 주어져 있다.
따라서 △AOO'은 SAS로 일단 모양새가 결정된 삼각형임을 알 수 있다. [2]
풀이
보통 쉬운 문제같으면 △AOO' 내부의 변이나 각을 세타로 표현한 뒤 극한을 때리면 그만이겠지만, 이 문제에서 구해야할 값은 선분 PQ이다.
따라서 PQ를 포함하는 어떠한 도형과 △AOO'의 내부 변이나 각을 공유하는 부분이 있는지를 살펴보아야 한다.
마침 삼각형 내심 성질에 따라 선분 AO'이 선분 PQ를 수직 이등분 한다. 각 이등분선을 그려서 자세히 관찰해보자.
선분 AO' (△AOO'이 결정되어있음은 아까 확인했다.) , 선분 PO' = 1, 각APO' =90º △APO'은 RHS로 결정되어있다.
그림과 같이 선분 PQ의 중점을 H라고 하면, △APO'과 △PHO'은 AA 닮음이다.
△PHO'이 알려져 있음을 확인했으므로, PQ = 2PH로 구할 수가 있다.
견적은 다 냈으니 이제 계산에 들어가자.
따라서 답은 3번이다.
평가
일단 먼저 선결정된 점 세개(삼각형) 부터 시작해서 목표 지점으로 차근차근 건너가는 자세가 중요하다.
그냥 냅다 임의의 각을 잡고 푸는 풀이도 있지만, 차근차근 넘어가는 방식이 더 필연적이고 실전적이라고 생각하여 이 풀이를 적었다.
삼각함수와 극한문제는 수능에서는 거의 꽁으로 주는 문항이고 다들 다 맞추는 문항이다. 절대 틀리지 않도록 많이 연습하자.