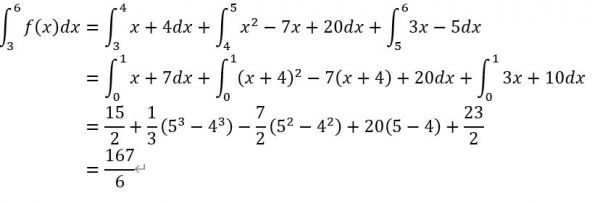|
이 적절한 문서는 적절합니다. 이 적절한 문서의 적절한 내용은 적절히 적절하기 때문에 적절하지 않은 당신도 적절히 적절하게 됩니다. |

|
이 문서는 이해하기 어려운 대상을 다룹니다. 이 문서는 일반적인 뇌를 가지고도 이해하기 어려운 대상에 대해 다룹니다. 두뇌를 풀가동해도 아마 이해하기 어려울 것입니다. |

|
개요
2015학년도 6월 평가원 모의고사 수학 B형 30번 문항이다.
문제 분석
f(x)에 대해서
f(x)는 미분가능한 것 말고는 아무것도 모르는 미지의 함수이다... 그리고 조건이 주렁주렁 달려있는데 저걸로 구해야하나보다.
구하라는 값
우리는 f(x)의 식을 완벽하게 알아내서 3부터 6까지 정적분을 때려야하나보다.
열심히 알아보자.
조건 해석
(가) 조건 해석
모든 실수 x에 대해서 1 ≤ f'(x) ≤ 3라고 한다.
일단 f(x)가 증가함수인건 알겠다. 근데 부등식 조건이라 먼저 건들여볼만한 조건은 아닌 것 같다.
등식조건이 좋잖아? 쑤셔 박으면 반응이 바로 오는 등식 조건이 ㅇㅇ
(나) 조건 해석
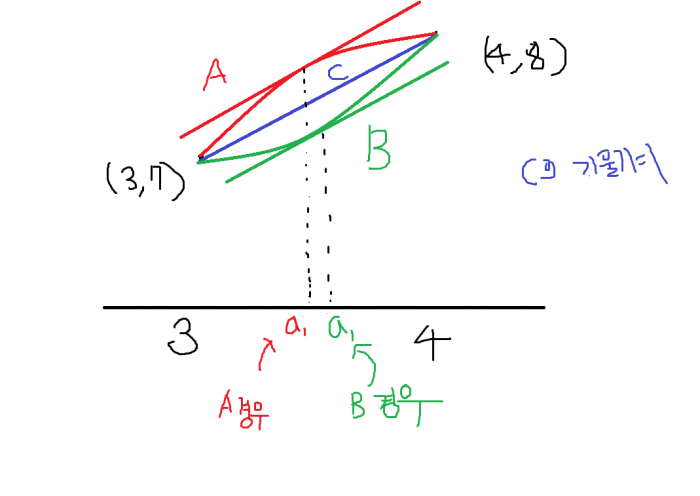
모든 정수 n에 대하여 점 (4n, 8n), 점 (4n + 1, 8n + 2) 점 (4n + 2, 8n + 5) 점 (4n + 3, 8n + 7)을 모두 지난다고 한다.
다른건 다 좆까고, 점을 지나? 우리가 찾던 등식 조건이다. 아까 적분구간이 3~6 이었으니까 x = 3, 4, 5, 6까지는 점을 구해보자.
적당히 각 점에 n에 0과 1을 대입해서 구하다 보면 (3, 7), (4, 8), (5, 10), (6, 13), 네 개의 점을 f(x)가 지남을 알 수 있다.
(다) 조건 해석
모든 정수 k에 대해서 닫힌 구간 [2k, 2k + 1]에서 f(x)가 이차함수
우리가 구해야하는 f(x)의 정의역 중 저 조건이 겹치는 부분은 닫힌 구간 [4, 5] 뿐 이다.
근데 임의의 이차함수 (ax2 + bx + c) 하나를 완벽하게 결정하는데 필요한 등식 개수는 3개이다.
근데 우리는 이미 f(4) = 8, f(5) = 10 임을 아니까, 이차함수의 미지수를 적어도 한개까진 줄여볼 수 있겠다.
풀이
Phase 1
일단 (다) 조건에서 알아낸 것들을 마무리부터 해보자.
닫힌 구간 [4, 5]에서 f(x)는 이차함수의 개형을 띤다고 한다.
그 이차함수를 임의로 p(x)라고 하자, [1]
p(x) = ax2 + bx + c 라고 하고, p(4) = 8, p(5) = 10 을 대입하자.
16a + 4b + c = 8, 25a + 5b + c = 10 이고
b, c를 a에 대해서 정리하면
b = 2 - 9a, c = 20a 이다.
따라서 p(x) = ax2 + (2 - 9a)x + 20a 이다.
Phase 2
일단 닫힌 구간 [4, 5]에서 얻을만한 f(x)의 조건은 다 구한 것 같다.
나머지 구간에서도 좀 살펴보도록 하자.
우선 닫힌 구간 [3, 4]에서 따져보자. 주어진 조건은
1) f(x)는 미분가능하다.
2) 1 ≤ f'(x) ≤ 3
3) f(3) = 7, f(4) = 8
이 정도인데... 어찌되었건 미분계수와 관련된 조건이 여러개 주어졌다.
뭔가 기울기 어쩌고 느낌이니까 여기서 잠시 닫힌 구간 [3, 4]에서의 f(x)의 평균변화율이라도 구해보자.
f(4) - f(3)4 - 3 = 1
놀랍게도 f'(x)의 최솟값이 툭 튀어나왔다...
f(x)는 미분가능한 함수이므로, 평균값 정리에 따라서
f(4) - f(3)4 - 3 = 1 = f'(a1) 을 만족하는 a1이 (3 < a1 < 4)에 적어도 하나 존재한다.
여기서 가능한 케이스를 하나씩 따져보자.
(A) f(x)가 닫힌 구간 [3, 4]에서 위로 볼록인 경우... f"(x) < 0
f'(a1) = 1일때, f"(x) < 0 이므로 f'(x)가 a1 < x < 4에서 감소한다.
f'(c) < 1인 c가 존재하게 되므로, "1 ≤ f'(x) ≤ 3" 조건에 위배된다. 고로 모순.
(B) f(x)가 닫힌 구간 [3, 4]에서 아래로 볼록인 경우... f"(x) > 0
f'(a1) = 1일때, f"(x) > 0 이므로 f'(x)가 3 < x < a1에서 증가한다.
f'(c) < 1인 c가 존재하게 되므로, "1 ≤ f'(x) ≤ 3" 조건에 위배된다. 고로 모순.
(C) f(x)가 닫힌 구간 [3, 4]에서 직선인 경우... f"(x) = 0
f(x)가 직선인 경우에는 위의 조건을 모두 만족한다.
따라서 f(x)는 닫힌 구간 [3, 4]에서 기울기가 1인 직선이다.
이젠 닫힌 구간 [5, 6]도 한번 조사해보자.
닫힌 구간 [5, 6]에서 주어진 조건은
1) f(x)는 미분가능하다.
2) 1 ≤ f'(x) ≤ 3
3) f(5) = 10, f(6) = 13
여기서도 닫힌 구간 [5, 6]에서의 f(x)의 평균변화율을 구해보면,
f(6) - f(5)6 - 5 = 3
아니나 다를까 여기는 f'(x)의 최댓값이다.
위에서 적용했던 논리대로 여기서도 따져주면 여기도 기울기가 3인 일차함수임을 알 수 있다.
따라서 f(x)는 닫힌 구간 [3, 4], [5, 6]에서 직선이다.
Phase 3
이제 지금까지 얻은 정보를 바탕으로 실제 f(x)의 식을 구해보자.
1) f(x)는 닫힌 구간 [3, 4]에서 (3, 7)을 지나고 기울기가 1인 일차함수이다. [2]
따라서 닫힌 구간 [3, 4]에서 f(x) = (x - 3) + 7 = x + 4
2) f(x)는 닫힌 구간 [5, 6]에서 (5, 10)을 지나고 기울기가 3인 일차함수이다.
따라서 닫힌 구간 [5, 6]에서 f(x) = 3(x - 5) + 10 = 3x - 5
3) f(x)는 실수 전체에서 미분 가능한 함수이다.
닫힌 구간 [4, 5]에서 f(x) = p(x) = ax2 + (2 - 9a)x + 20a
미지수가 한개이므로 등식 하나만 더 있으면 된다.
p'(x) = 2ax + 2- 9a 이고,
p'(4) = f'(4) = 1이므로,
a = 1, p(x) = x2 - 7x + 20 이다.
따라서 f(x)는 다음과 같다.
(3≤x≤4)... f(x) = x + 4
(4≤x≤5)... f(x) = x2 - 7x + 20
(5≤x≤6)... f(x) = 3x - 5
구하고자 하는 값을 계산하면
a = 1676이므로 6a = 167
답은 167이다.
평가
격자점 찍어서 미지의 함수를 추론하는... 해괴망칙한 문제다.
문제 참 잘만들었다고 생각하는게 "ㄱ,ㄴ,ㄷ" 문항에서만 쓰이던 평균값정리를 주관식 문항에 어느정도 잘 녹여낸 문제이다.
물론 그런거 생각 안하고 대충 감으로 "직선이겠네" 하고 찍은 사람이 더 많다.
개인적으로는 평가원 성선설이 잘 드러났던 문제이다.
n에 모든 정수를 넣을 수 있다. 즉, 구간을 3부터 6까지가 아니라 뭐 50, 60까지 늘려도 할 말 없는 문제였는데 교수가 그건 너무하다 싶었나 보다. 그래서 난이도가 많이 높진 않다.