순열

주의. 이 문서는 심히 진지하여 노잼일 수 있습니다.
이 글은 놀랍게도 디시위키에서 진지를 빨고 있습니다. 노잼이다 싶으시면 여기를 클릭하시어 이 문서를 탈출할 수 있습니다.

“

서로 다른 n개의 원소에서 r개를 중복없이 골라 순서에 상관있게 나열하는 것을 n개에서 r개를 택하는 순열이라고 한다.

”

상위문서: 수학

설명

Permutation(펄뮤테이션)

기호로는 _nP_r이 있다. 이 기호가 존나게 쓰인다.

사실 이건 초딩 때 배웠을 거다. 예로 들어 0, 2,3,5 이 네장의 카드를 이용하여 세자리 수의 갯수를 구하시오. 라던가 최단경로 문제라던가...

! ←이 느낌표는 팩토리얼이라고 한다. 줄여서 팩.

5! (오팩) 5×4×3×2×1=120

0!=1이다.

중복 순열

n개에서 r를 순서대로 쳐뽑는데 중복을 허락하여 쳐뽑는거다. 초딩 때 한번 쯤 한 기억이 날 거다. 그게 중복 순열인줄은 그 당시엔 몰랐겠지..? 지수를 사용해 경우의 수를 나타내면 n^r이 된다.

세계적으로는 걍 n^r 이렇게 쓰지만 머한민국에서는 _nΠ_r(여기서Π는 product라는 글자 첫 글자p에 해당되는 그리스 문자 '파이')의 기호를 쓰고 뒤에 저걸 적는다...

같은 것이 있는 경우의 순열(동자 순열)

n개 중에 r개를 중복없이 순서에 맞게 뽑는데, n개 중에 똑같은 것이 몇개 섞여있을 경우를 말한다. 예로 들어 이런거.

aaabbcd

7!/3!2!

공식은 (p₁+p₂+p₃+...p_n)!/p₁!×p₂!×p₃!×...p_n!

최단 경로

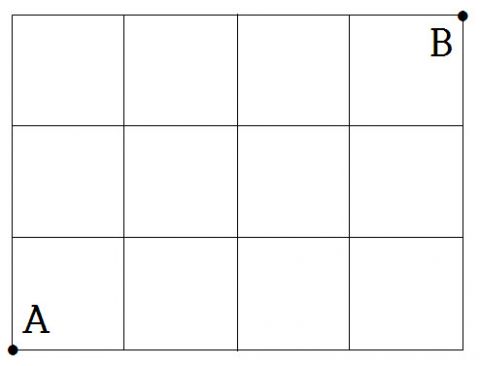
이게 뭔지 알지..? 초중딩 때 가로세로에 1을 쳐넣고 구했던 그거다. 예로 들어 A에서 B를 최단 경로로 갈 수 있는거라든지 중간에 P가 낑겨있을 때 거치고 지나가라든지 안거치고 지나가라든지...

가끔 웅덩이 같은게 있다. 웅덩이 극혐. 아.. 그리기 귀찮다.

위 짤보니 뭔지 알겠지..? aaaa(가로)bbb(세로)

원순열

원탁에 쳐앉자. (공식 (n-1)!)서로 다른 n개를 원형으로 배열할 때만 쓰인다.

아직 안배운 놈들은 "고정"을 유의해라. 고정을 했으면 일단 뱅글뱅글 돌려보자.

활용

다각형 순열

삼각형, 정사각형과 직사각형이 대표적. 직사각형은 헷갈릴 수도 있다.

육각형 나오면 히오스 아이콘으로 낙서하는 새끼들 있을거다. 그 새끼가 진짜 시공충인지는 무한한 공간 저 너머로....

뒤집어 놓을 수 있는 원순열의 수

염주순열, 목걸이순열이라고도 불린다.

공식 (n-1)!/2 ㄴ 때에따라 저거 아닐때도있음 규칙적으로 놓여져있다던가

완전 순열

자기 것을 가지지 않는 패턴 유형이다. 외워두면 편하다.

0 1 2 9 44

ㅇㅇ 그러하다.

여담

확통에서 조합이랑 같이 나오는 놈이기도 하다. 이거 모르거나 기억력이 병신되어 까먹으면 확통 반의 반이나 반쯤은 버렸다고 생각하자.

설명