(파푸스의 중선 정리에서 넘어옴)
파일:Crystal Clear app xmag.svg 스튜어트 정리 문서를 참고하십시오.

|
01 문서ㄴㄴ 수학과 관련된 것ㅇㄹ 다룹니다. 01 문서ㄴㄴ 수학과 관련된 무언7ㅏ0ㅔ 대해서 다루ㄴㄴ 문서입니다. ㄱㅂ식 수학일 수도 전공 수학일 수도 있고, 혹ㅇㄴ 수학과 관련된 역사속의 인물일지도 모ㄹㅂ니다. 01 문서ㄹㄹ 읽다7ㅏ 수학뽕0ㅔ 빠져버려도 본 위키ㄴㄴ 책임지지 않ㅅㅂ니다. 1 + 1 = 귀요미>_< |
개요
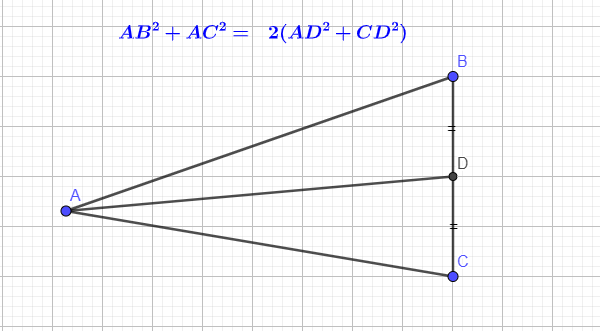
Apollonius' theorem
스튜어트 정리의 하위호환이다. 스튜어트 정리에서 중선을 분할하는 형태면 아폴로니오스 정리가 된다.
헬조센과 좆본에서는 "파푸스의 중선 정리"라는 해괴망칙한 이름으로 부르고 있다.
증명
스튜어트 정리의 증명에서 분할되는 점을 변의 중점으로만 바꾸면 아폴로니오스의 정리의 증명도 되므로 그쪽 문서도 참조해보도록.
여기서는 합동을 이용한 증명을 해보겠다.
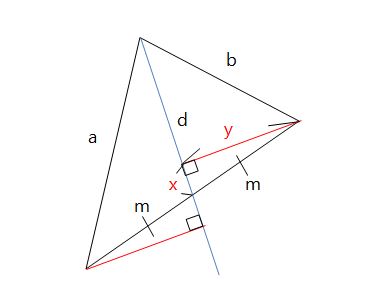
중선을 연장한 후 나머지 꼭지점에서 수선을 내린다.
이때 두 삼각형은 세 각이 같고 대응되는 변의 길이가 m으로 같으므로 RHA 합동이다.
a2 = y2 + (d + x)2
b2 = y2 + (d - x)2
두 식을 더하면
a2 + b2 = 2y2 + 2d2 + 2x2
a2 + b2 = 2(d2 + m2)
증명 끗